결정론적 모델의 표기법과 분류 방법 | Scheduling 002

Scheduling 의 이전 글 읽기 

서론 - 스케줄링의 역할과 기능 | Scheduling 001

서론 - 스케줄링의 역할과 기능 | Scheduling 001

 

결정론적 모델 (Deterministic Models) 

결정론적 스케줄링 모델은 모든 작업의 시작과 종료 및 기간이 결정되어 있고, 정확한 추청치가 있는 비교적 간단한 스케줄링 모델이다. 이러한 결정론적 모델의 주요 장점으로는 1) 단순성및 명확성, 2) 제어의 용의성, 3) 예측 가능한 프로젝트에 적합하다는 것과 4) 효율적인 추적이 가능하다는 점을 들 수 있으며, 주요 단점으로는 1) 유연성 부족, 2) 추정치에 대한 과신 및 3) 불확실한 환경에는 적합하지 않음을 들 수 있다. 

 

표기법 (Notation) 

모든 결정론적 스케줄링 문제에서 고려하는 작업 (jobs) 의 수, $n$ 과 자원 또는 기계 (machines) 의 수, $m$ 은 유한하다고 가정한다. 일반적으로 접미사 $j$ 는 작업과, 접미사 $i$ 는 기계와 관련된다. 다음은 작업 $j$ 와 연관된 표기법의 설명이다. 

 

• Processing time $(p_{ij})$: 기계 $i$ 에서 작업 $j$ 의 처리 시간, 작업 $j$ 의 처리 시간이 기계에 의존하지 않거나 지정된 기계 하나에서만 처리되는 경우 접미사 $i$ 는 생략될 수 있음.
• Release date $(r_{j})$: 작업 $j$ 의 준비 날짜 또는 도착 날짜 $r_{j}$ 는 작업이 시스템에 도착하는 시간, 즉 작업 $j$ 가 처리를 시작할 수 있는 가장 빠른 날짜를 의미함.
• Due date $(d_{j})$: 작업 $j$ 의 마감일 $d_{j}$ 는 약속된 배송일 또는 완료일을 의미하며, 마감일 이후에 작업을 완료하는 것은 일반적으로 허용되지만 페널티가 부과될 수 있음. 마감일을 반드시 지켜야 하는 경우, 이를 Deadline 이라고 하며 $\overline{d_{j}}$ 로 표시됨.
• Weight $(w_{j})$: 작업 $j$ 의 가중치 $w_{j}$ 는 시스템에서 작업 $j$ 의 중요성을 나타냄.

 

 

스케줄링 문제의 분류: $α \ | \ β \ | \ γ$

스케줄링 문제는 $α \ | \ β \ | \ γ$ 의 삼중항으로 분류할 수 있다. 

 

• $α$ 필드는 기계 환경을 설명하며, 하나의 항목만 포함. 
• $β$ 필드는 처리 특성 및 제약 조건에 대한 세부 정보를 제공하며 항목이 전혀 없거나, 단일 항목 또는 여러 항목을 포함.
• $γ$ 필드는 스케줄링 문제의 목적 함수를 설명하며, 대체로 단일 항목을 포함.

 

$α$ 필드

$α$ 필드에 지정할 수 있는 기계 환경과 (표시 기호) 는 아래에서 보는 바와 같다. 

 

• Single machine $(1)$ : 기계 환경 중 가장 단순한 경우이며, 앞으로 설명할 다른 모든 기계 환경들의 special case 라고도 볼 수 있다. 
• Identical machines in parallel $(Pm)$ : 동일한 $m$ 개의 기계가 병렬로 연결된 경우이며, $m$ 대의 기계 중 하나 또는 특정 부분 집합 $M_{j}$ 에 속하는 기계에서 처리될 수 있다. 후자의 경우, $β$ 필드에 $M_{j}$ 가 표시된다. 
• Machines in parallel with different speeds $(Qm)$ : 속도가 서로 다른 기계가 병렬로 배치된 경우이며, uniform machines environment 라고도 표현한다. 기계 $i$ 의 속도는 $v_{i}$ 로 표시되고, 작업 $j$ 가 기계 $i$ 에서 처리되는 시간 $p_{ij}$ 는 $p_{j}/v_{i}$ 와 같다 (작업 $j$ 가 기계 $i$ 에서 모든 처리를 받는다고 가정). 만약 모든 기계의 속도가 같다면, 이 환경은 "identical machines in parallel" 과 동일하다. 
• Unrelated machines in parallel $(Rm)$ : 이 환경은 병렬로 연결된 여러 대의 기계가 있으며, 기계 $i$ 는 작업 $j$ 를 속도 $v_{ij}$로 처리한다. 작업 $j$ 가 기계 $i$ 에서 처리되는 시간 $p_{ij}$ 는 $p_{j}/v_{i}$ 와 같다 (작업 $j$ 가 기계 $i$ 에서 모든 처리를 받는다고 가정). 기계의 속도가 작업과 무관하게 독립적인 경우, 즉 모든 $i$ 와 $j$ 에 대해 $v_{ij} = v_{i}$ 인 경우, 이 환경은 "machines in parallel with different speeds" 과 동일하다.
• Flow shop $(Fm)$ : 이 환경은 여러 대의 기계가 직렬로 연결되어 있으며, 모든 작업은 동일한 경로 (route) 를 따라야 한다. 한 기계에서 작업이 완료되면 다음 기계의 대기열 (queue) 에 합류한다. 일반적으로 모든 대기열은 FIFO (first in first out) 를 따르는 것으로 가정하는데, 이러한 경우 순열 (permutation) 플로우 샵이라고 하고 $β$ 필드에 $prmu$ 가 포함된다.
• Flexible flow shop $(FFc)$ : 이 환경은 flow shop 과 parallel machines 환경을 일반화한 것으로 hybrid flow shop 또는 multi-processor flow shop 이라고도 한다. 여러 대의 기계가 직렬로 배치되는 대신 각 단계마다 여러 대의 동일한 기계가 병렬로 배치되는 $c$ 개의  단계가 있다. 각 작업은 1단계에서 먼저 처리한 다음, 2단계에서 처리하는 식으로 진행된다. 한 단계가 병렬 기계의 묶음 역할을 하며, 각 단계에서 작업 $j$ 는 한 대의 기계에서만 처리되어야 하고 어떤 기계에서든 처리될 수 있다. 여러 단계 사이의 대기열은 FIFO 원칙에 따라 운영될 수도 있고 그렇지 않을 수도 있다.
• Job shop $(Jm)$ : 각 작업은 미리 정해진 각각의 경로가 있으며, 크게 한 작업이 각 기계를 최대 한 번만 방문하는 job shop 과 한 작업이 각 기계를 두 번 이상 방문할 수 있는 job shop 으로 구분된다. 후자의 경우 $β$ 필드에는 재순환을 의미하는 $rcrc$ 가 포함된다. 
• Flexible job shop $(FJc)$ : 이 환경은 job shop 과 parallel machines 환경을 일반화한 것이다. 직렬로 연결된 여러 대의 기계 대신 각 작업 센터에 여러 대의 동일한 기계가 병렬로 연결된 $c$ 개의 워크 센터 (work center) 가 있다. 각 작업은 고유한 경로가 있으며, 작업 $j$ 는 각 워크 센터에서 한 대의 기계로만 처리해야 하며 모든 기계가 수행할 수 있다. 작업이 워크 센터를 두 번 이상 방문할 수 있는 경우, $β$ 필드에는 재순환을 의미하는 $rcrc$ 가 포함된다. 
• Open shop $(Om)$ : 각 작업은 $m$ 개의 기계에서 각각 다시 처리되어야 하지만, 이러한 처리 시간 중 일부는 0이 될 수도 있다. 각 작업의 경로에는 제한이 없으며, 이는 스케줄러가 각 작업의 경로를 결정할 수 있고, 작업마다 다른 경로를 가질 수 있음을 뜻한다. 

 

 

$β$ 필드 

$β$ 필드에 지정된 처리 제한 및 제약 조건에는 여러 항목이 포함될 수 있으며, 아래에서 보는 바와 같다.

 

• Release dates $(r_{j})$ : 이 기호는 작업 $j$ 가 $r_{j}$ 이후에 처리를 시작할 수 있음을 뜻한다. 이 기호가 없는 경우, 작업 $j$ 는 언제든지 처리를 시작할 수 있다. 
• Preemptions $(prmp)$ : 이 기호는 처리 중인 작업을 완료되기 전에 중단시킬 수 있음을 뜻한다. $β$ 필드에 $prmp$ 가 있다면, 스케줄러는 언제든지 작업의 처리를 중단하고 대신 다른 작업을 기계에 넣을 수 있다. 선점된 작업이 이미 받은 처리량은 손실되지 않으며, 선점된 작업이 나중에 다시 기계에 배치되면 남은 처리 시간 동안만 해당 기계가 필요하다.
• Precedence constraints $(prec)$ : 선행 제약은 특정 작업이 처리를 시작하기 전에 하나 이상의 선행 작업이 완료되어야 하는 조건이 있음을 뜻한다. 
• Sequence dependent setup times $(s_{jk})$ : $s_{jk}$ 는 작업 $j$ 와 작업 $k$ 의 처리 사이에 발생하는 설정 시간을 나타내며, 작업 $k$ 가 시퀀스에서 첫 번째인 경우 작업 $k$ 의 설정 시간을, 작업 $j$ 가 시퀀스에서 마지막인 경우 작업 $j$ 이후의 정리 시간을 나타낸다 (물론 $s_{0k}$ 와 $s_{j0}$ 은 0일 수도 있음). 작업 $j$ 와 작업 $k$ 사이의 설정 시간이 기계에 따라 다른 경우에는 아래 첨자 $i$ 가 포함되어 $s_{ijk}$ 의 형태로 표시된다. 
• Job families $(fmls)$ : $n$ 개의 작업이 서로 다른 $F$ 개의 작업 패밀리에 속하는 경우, 기계가 한 패밀리에서 다른 패밀리 (예: 패밀리 $g$ 에서 패밀리 $h$) 로 전환될 때에는 일반적으로 설정 시간이 필요하다. 이 설정 시간이 패밀리 $g$ 와 $h$ 모두에 의존하고 시퀀스에 따라 달라지면 $s_{gh}$ 로 표시하고, 이 설정 시간이 시작하려는 패밀리 (예: 패밀리 $h$) 에만 의존하면 $s_{h}$ 로 표시한다. 어느 패밀리에도 의존하지 않는다면 $s$ 로 표시한다. 
• Batch processing $(batch(b))$ : 기계가 여러 개의 작업을 동시에 처리할 수 있는 경우에 해당하며, 배치에 포함된 작업의 처리 시간은 모두 같지 않을 수 있다. 배치의 마지막 작업이 완료되어야만 전체 배치가 완료되므로 배치 완료 시간은 처리 시간이 가장 긴 작업에 의해 결정된다. 
• Breakdowns $(brkdwn)$ : 기계 고장은 기계를 지속적으로 사용할 수 없음을 의미하며, 때때로 기계 가용성 제약이라고도 한다. 기계를 사용할 수 없는 기간은 교대 근무 또는 예정된 유지 보수 등으로 인해 고정된 것으로 가정한다. 동일한 기계가 병렬로 여러 대 있는 경우, 특정 시점에 사용 가능한 기계의 수는 시간의 함수 $m(t)$ 이다. 
• Machine eligibility restrictions $(M_{j})$ : 이 기호는 작업 $j$ 를 처리할 수 있는 머신의 집합을 나타낸다.  
• Permutation $(prmu)$ : flow shop 환경에서 각 기계 앞의 대기열이 FIFO 원칙에 따라 작동하는 경우를 뜻한다.
• Blocking $(block)$ : 블로킹이란 완료된 작업이 기계에 남아 있어 해당 기계가 다음 작업을 진행하지 못하도록 막는 현상을 나타내며, 일반적으로 flow shop 에서 주로 발생한다. 
• No-wait $(nwt)$ : 작업은 두 개의 연속된 기계 사이에서 대기할 수 없음을 뜻한다. 이러한 작업의 예로 철강 압연 공장을 들 수 있는데, 대기 중에 철강 슬래브가 식을 수 있기 때문이다. 일반적으로 flow shop 에서 주로 발생한다. 
• Recirculation $(rcrc)$ : 작업이 기계 또는 워크 센터를 두 번 이상 방문할 수 있는 경우 재순환이 발생할 수 있다. 일반적으로 job shop 또는 flexible job shop 에서 주로 발생한다. 

 

$γ$ 필드 

$β$ 필드에는 스케줄링 문제의 목적 함수가 포함되며, 이를 설명하기 위해 아래의 몇 가지 개념 이해가 필요하다. 

 

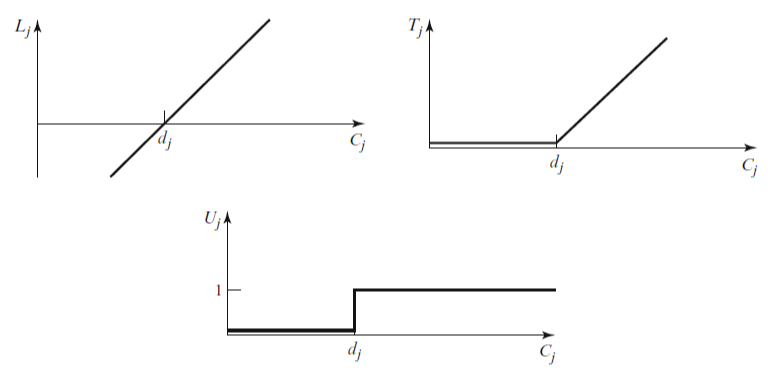
• Completion time of job $j$ $(C_{j})$ 
• Lateness of job $j$ $(L_{j}= C_{j}-d_{j})$
• Tardiness of job $j$ $(T_{j}=max(C_{j}-d_{j},0)=max(L_{j},0))$
• Unit penalty of job $j$ $(U_{j}=1 \; if \; C_{j}>d_{j}, \; 0 \; otherwise)$

 

$C_{j}$ 에 따른 $L_{j}, \; T_{j} \;$ 및 $U_{j}$ 의 그래프는 아래 그림에서 보는 바와 같다. 

 

 

$C_{j}, \; L_{j}, \; T_{j} \;$ 및 $U_{j}$ 를 이용하여 계산되는 목적 함수의 예는 아래와 같다. 

 

• Makespan $(C_{max})$ : 시스템을 떠나는 마지막 작업의 완료 시간과 같으며, $max(C_{1}, . . . , C_{n})$ 으로 정의된다. 일반적으로 makespan 이 최소라는 것은 기계의 활용도가 높다는 것을 의미한다.  
• Maximum Lateness $(L_{max})$ : 마감일 또는 마감시간을 가장 심하게 위반한 시간을 측정하며, $max(L_{1}, . . . , L_{n})$ 으로 정의된다. 
• Total weighted completion time $(\sum w_{j}C_{j})$ : $n$ 개 작업의 가중 완료 시간의 합은 일정에 의해 발생한 총 보유 또는 재고 비용을 나타낸다.
• Discounted total weighted completion time $(\sum w_{j}(1-e^{-rC_{j}}))$ : Total weighted completion time 보다 더 일반적인 비용 함수이며, 단위 시간당 $r \; (0 <r <1)$ 의 비율로 비용이 할인되는 차이점이 있다. 작업 $j$ 가 시간 $t$ 까지 완료되지 않으면 $[t, \; t + dt]$ 기간 동안 추가 비용 $w_{j}re^{-rt}dt$ 가 발생한다. 만약 작업 $j$ 가 시간 $t$ 에 완료되면 기간 $[0, \; t]$ 동안 발생한 총 비용은 $w_{j}(1-e^{-rt})$ 이다. $r$ 의 값은 일반적으로 0에 가깝게, 예를 들어 0.1 또는 10% 이다.
• Total weighted tardiness $(\sum w_{j}T_{j})$ : Total weighted completion time 보다 더 일반적인 비용 함수이다. 
• Weighted number of tardy jobs $(\sum w_{j}U_{j})$ : 매우 쉽게 기록할 수 있는 척도 중의 하나이다. 

 

참고문헌 

M. Pinedo (2016), Scheduling: Theory, Algorithms, and Systems - Fifth Edition

 

Scheduling 의 다음 글 읽기 

(TBD)